5 Forward Chaining

This chapter discusses a forward chaining rule based system and its expert system applications. It shows how the forward chaining system works, how to use it, and how to implement it quickly and easily using Prolog.

A large number of expert systems require the use of forward chaining, or data driven inference. The most famous of these is Digital Equipment Corporation's XCON system. It configures computers. It starts with the data about the customer order and works forward toward a configuration based on that data. The XCON system was written in the OPS5 (forward chaining rule based) language.

Data driven expert systems are different from the goal driven, or backward chaining systems seen in the previous chapters.

The goal driven approach is practical when there are a reasonable number of possible final answers, as in the case of a diagnostic or identification system. The system methodically tries to prove or disprove each possible answer, gathering the needed information as it goes.

The data driven approach is practical when combinatorial explosion creates a seemingly infinite number of possible right answers, such as possible configurations of a machine.

5.1 Production Systems

Forward chaining systems are often called "production" systems. Each of the rules is actually a miniature procedure called a production. When the patterns in the left hand side match working storage elements, then the actions on the right hand side are taken. This chapter concentrates on building a production system called Oops.

Production systems are composed of three components. These are:

The rules are of the form:

The LHS is a collection of conditions which must be matched in working storage for the rule to be executed. The RHS contains the actions to be taken if the LHS conditions are met.

The execution cycle is:

Production systems differ in the sophistication of the algorithm used to select a rule (step 1). The first version of Oops will use the simplest algorithm of just selecting the first rule whose conditions match working storage.

The knowledge engineer programs in Oops by creating rules for the particular application. The syntax of the rules is:

where:

Each condition is a legal Prolog data structure, including variables. Variables are identified, as in Prolog, by an initial upper case letter, or underscore. In general, the condition pattern is matched against those stored in working storage. The comparison operators (>, =<, etc.) are also defined for comparing variables which are bound during the pattern matching.

Note that the data representation of Oops is richer than that used in Clam. In Clam there were only attribute - value pairs, or object - attribute - value triples. In Oops the data can be represented by any legal Prolog term including variables.

The following RHS actions are supported:

5.2 Using Oops

In the Winston & Horn LISP book there is an example of a forward chaining animal identification system. Some of those rules would be expressed in Oops like this:

This rule would fire if working storage contained the Prolog terms:

When the rule fired, these three terms would be removed by the retract(all) action on the RHS, and would be replaced with the term:

Since the working storage elements which matched the conditions were removed, this rule would not fire again. Instead, another rule such as this might fire next:

Rules about relationships are also easily coded. Again from Winston & Horn's example the rule which says children are the same type of animal as their parents is expressed as follows:

This would transform working storage terms like:

to:

The working storage is initialized with a statement of the form:

Each term is a legal Prolog term which is asserted in working storage.

For example:

It would be better if we could set up the system to ask the user for the initial terms. In a conventional programming language we might set up a loop which repeatedly asked for data until the user typed in "end".

To do the same thing in a production system requires a bit of trickery, which goes against the grain of rule based systems. Theoretically, the rules are independent and don't communicate with each other, but by setting flags in working storage the programmer can force a specific order of rule firings.

Here is how to code the input loop in Oops. It violates another tenet of production systems by making use of the known rule selection strategy. In the case of Oops, it is known that rule 1 will be tried before rule 2.

The animal identification problem is one that can be solved either in a data driven (forward chaining) approach as illustrated here and in Winston & Horn, or in a goal driven (backward chaining) approach. In fact, where the list of possible animals is known the backward chaining approach is probably a more natural one for this problem.

A more suitable problem for a forward chaining system is configuration. The Oops sample program in the appendix shows such a system. It lays out furniture in a living room.

The program includes a number of rules for laying out furniture. For example:

Here are those rules in Oops. They are more complex due to the need to work with the amount of wall space available.

The program also uses rules to control a dialog with the user to gather initial data. It needs to know about room dimensions, furniture to be placed, plug locations, etc. It does this by setting various data gathering goals. For example the initial goal of the system is to place_furniture. It gives directions to the user and sets up the goal read_furniture. Once read_furniture is done (signified by the user entering end : end), it sets up the next goal of read_walls. Here is the beginning code.

The room configurer illustrates both the strengths and weaknesses of a pure production system. The rules for laying out the furniture are very clear. New rules can be added, and old ones deleted without affecting the system. It is much easier to work with this program structure than it would be to understand procedural code which attempted to do the same thing.

On the other hand, the rules which interact with the user to collect data are difficult to read and have interdependencies which make them hard to maintain. The flow of control is obscured. This code would be better written procedurally, but it is done using Oops to illustrate how these kinds of problems can be solved with a production architecture.

An ideal architecture would integrate the two approaches. It would be very simple to let Oops drop back down to Prolog for those cases where Oops is inappropriate. This architecture is covered in chapter 7.

5.3 Implementation

The implementation of Oops is both compact and readable due to the following features of Prolog:

Each rule is a single Prolog term, composed primarily of two lists: the right hand side (RHS), and the left hand side (LHS). These are stored using Prolog's normal data structures, with rule being the predicate and the various arguments being lists.

In Clam, DCG was used to allow a friendly, flexible rule format. In Oops, Prolog operators are used. The operators allow for a syntax which is formal, but readable. The operator syntax can also be used directly in the code.

Without operator definitions, the rules would look like normal hierarchical Prolog data structures:

The following operator definitions allow for the more readable format of the rules:

Working storage is stored in the database under the key fact. So to add a term to working storage:

and to look for a term in working storage:

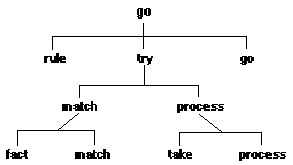
Figure 5.1 shows the major predicates in the Oops inference engine. The inference cycle of recognize - act is coded in the predicate go. It searches for the first rule which matches working storage, and executes it. Then it repeats the process. If no rules match, then the second clause of go is executed and the inference ends. Then the second clause prints out the current state showing what was determined during the run. (Note that LHS and RHS are bound to lists.)

Figure 5.1. Major predicates in Oops inference engine

This code illustrates the tremendous expressiveness of Prolog. The code is very tight due to the built-in pattern matching and backtracking search. Especially note that since the entire rule is a single Prolog term, the unification between variables in the conditions and actions happens automatically. This leads to a use of variables which is, in some senses, cleaner and more powerful than that found in OPS5.

The try/2 predicate is very simple. If match/2 fails, it forces go to backtrack and find the next rule. The LHS is passed to process so retract statements can find the facts to retract.

The match/2 predicate recursively goes through the list of conditions, locating them in working storage. If the condition is a comparison test, then the test is tried, rather than searched for in the database.

The test/1 predicate can be expanded to include any kind of test. Oops uses most of the basic tests provided with Prolog, plus a few. For example:

If match/2 succeeds, then process/2 is called. It executes the RHS list of actions. It is equally straightforward.

Only the action retract needs the LHS. The take/2 predicate does a retract if that is what's called for, or else passes control to take/1 which enumerates the simpler actions. Some examples are given here.

The retr predicate searches for LHS conditions with the same identification (N) and retracts them. If all was indicated, then it retracts all of the LHS conditions.

Oops can be made to look like the other shells by the addition of a command loop predicate with commands similar to those in Clam and Native. Figure 5.2 shows the architecture of Oops.

5.4 Explanations for Oops

Explanations for forward chaining systems are more difficult to implement. This is because each rule modifies working storage, thus covering its tracks. The most useful information in debugging a forward chaining system is a trace facility. That is, you want to know each rule that is fired and the effects it has on working storage.

Each fact can have associated with it the rule which posted it, and this would give the immediate explanation of a fact. However, the facts which supported the rules which led up to that fact might have been erased from working memory. To give a full explanation, the system would have to keep time stamped copies of old versions of facts.

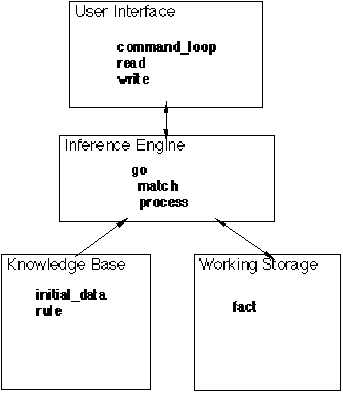
Figure 5.2. Major predicates of the Oops shell

The trace option is added in Oops in a similar fashion to which it was added in Clam. The inference engine informs the user of the rules which are firing as they fire.

5.5 Enhancements

Oops in its current state is a simple forward chaining system. More advanced forward chaining systems differ in two main aspects.

The current rule selection strategy of Oops is simply to pick the first rule which matches. If many rules match, there might be other optimal choosing strategies. For example, we could pick the rule that matched the most recently asserted facts, or the rule which had the most specific match. Either of these would change the inference pattern of the system to give effects which might be more natural.

Oops is also inefficient in its pattern matching, since at each cycle of the system it tries all of the rules against working memory. There are various indexing schemes which can be used to allow for much faster picking of rules which match working memory. These will be discussed in the chapter 8.

5.6 Rule Selection

OPS5, which is probably the most well known example of a forward chaining, or production, system offers two different means of selecting rules. One is called LEX and the other is MEA. Both make use of time stamped data to determine the best rule to fire next. They differ slightly in the way in which they use the data. Both of these strategies can be added to Oops as options.

Generating the conflict set

For both, the first step is to collect all of the rules whose LHS match working memory at a given cycle. This set of rules is called the conflict set. It is not actually the rules, but rather instantiations of the rules. This means that the same rule might have multiple instantiations if there are multiple facts which match a LHS premise. This will often happen when there are variables in the rules which are bound differently for different instantiations.

For example, an expert system to identify animals might have the following condition on the LHS:

In working memory there might be the following two facts:

Assuming the other conditions on the LHS matched, this would lead to two different instantiations of the same rule. One for robie and one for suzie.

The simplest way to get the conflict set is to use findall or its equivalent. (If your system does not have a findall, a description of how to write your own can be found in Clocksin and Mellish section 7.8, Assert and Retract: Random, Gensym, Findall.) It collects all of the instantiations of a term in a list. The three arguments to findall are:

The instantiations of the conflict set will be stored in a structure, r/4. The last three arguments of r/4 will be the ID, LHS, and RHS of the rule which will be used later.

The first argument of r/4 is the LHS with the variables instantiated with the working storage elements that were matched. Each match of a LHS premise and working storage element is also accompanied by a time stamp indicating when the working storage element was last updated.

The query to be executed repeatedly by findall will be similar to the one currently used to find just the first matching rule:

Note that match now has a second argument to store the instantiation of the rule which will be the first argument to r/4.

The following predicate puts the above pieces together and uses findall to build a list (CS) of r/4s representing all of the rules which currently match working storage.

The match predicate just needs to be changed to capture the instantiation of the conditions. Notice there is an additional argument, Time, in the fact predicate. This is a time stamp that will be used in the selection process.

Time stamps

The timestamp is just a chronological counter that numbers the facts in working memory as they are added. All assertions of facts are now handled by the assert_ws predicate as follows:

The getchron predicate simply keeps adding to a counter.

5.7 LEX

Now that we have a list of possible rules and instantiations in the conflict set, it is necessary to select one. First we will look at the OPS5 LEX method of rule selection. It uses three criteria to select a rule.

The first is refraction. This discards any instantiations which have already been fired. Two instantiations are the same if the variable bindings and the time stamps are the same. This prevents the same rule from firing over and over, unless the programmer has caused working memory to be repeatedly updated with the same fact.

The second is recency. This choses the rules which use the most recent elements in working memory. The conflict set rules are ordered with those rules with the highest time stamps first. This is useful to give the system a sense of focus as it works on a problem. Facts which are just asserted will most likely be used next in a rule.

The third is specificity. If there are still multiple rules in contention, the most specific is used. The more conditions there are that apply in the LHS of the rule, the more specific it is. For example, a rule with 4 conditions is more specific than one with 3 conditions. This criteria ensures that general case rules will fire after more specific case rules.

If after these tests there are still multiple rules which apply, then one is chosen at random.

Changes in the Rules

The LEX strategy changes the way in which Oops rules are programmed. In the first version of Oops, the knowledge engineer had to make sure that the working storage elements which caused the rule to fire are changed. It was the knowledge engineer's responsibility to ensure that a rule did not repeatedly fire.

The opposite is also true. Where looping is required, the facts matching the LHS must be continually reasserted.

In the original version of Oops the knowledge engineer knew the order in which rules would fire, and could use that information to control the inference. Using LEX he/she can still control the inference, but it requires more work. For example, if it is desirable to have the couch placed first by the system, then that rule must be structured to fire first. This can be done by adding a goal to place the couch first and asserting it after the data is gathered. For example:

The gather_data rule will assert the couch_first goal after all other assertions. This means it is the most recent addition to working storage. The Lex recency criteria will then ensure that the couch rule is fired next.

The rule which is supposed to fire last in the system also needs to be handled specially. The easiest way to ensure a rule will fire last is to give it an empty list for the LHS. The specificity check will keep it from firing until all others have fired.

Implementing LEX

To implement the LEX strategy, we modify the go predicate to first get the conflict set and then pass it to the predicate select_rule which picks the rule to execute. After processing the rule, the instantiation associated with the rule is saved to be used as a check that it is not reexecuted.

The select_rule predicate applies the three criteria above to select the appropriate rule. The refract predicate applies refraction, and lex_sort applies both recency and specificity through a sorting mechanism.

First let's look at refract, which removes those rules which duplicate existing instantiations. It relies on the fact that after each successful rule firing, the instantiation is saved in the database.

Once refract is done processing the list, only those rules with new instantiations are left on the list.

The implementation of lex_sort doesn't filter the remaining rules, but sorts them so that the first rule on the list is the desired rule. This is done by creating a key for each rule which is used to sort the rules. The key is designed to sort by recency and specificity. The sorting is done with a common built-in predicate, keysort, which sorts a list by keys where the elements are in the form: key - term. (If your Prolog does not have a keysort, see Clocksin and Mellish section 7.7, Sorting.)

The build_keys predicate adds the keys to each term. The keyed list is then sorted by keysort. It comes out backwards, so it is reversed, and finally the keys are stripped from the list. In order for this to work, the right key needs to be chosen.

The key which gives the desired results is itself a list. The elements are the time stamps of the various matched conditions in the instantiation of the rule. The key (a list) is sorted so that the most recent (highest number) time stamps are at the head of the list. These complex keys can themselves be sorted to give the correct ordering of the rules. For example, consider the following two rules, and working storage:

There would be two instantiations of the first rule, one each for lara and zach, and one instantiation of the second rule for bonbon. The highest numbers are the most recent time stamps. The keys (in order) for these three instantiations would be:

In order to get the desired sort, lists must be compared element by element starting from the head of the list. This gives the recency sort. The sort must also distinguish between two lists of different lengths with the same common elements. This gives the specificity sort. For AAIS prolog the sort works as desired with recency being more important than specificity. It should be checked for other Prologs.

Here is the code to build the keys:

The build_keys predicate uses build_chlist to create a list of the time stamps associated with the LHS instantiation. It then sorts those, and reverses the result, so that the most recent time stamps are first in the list.

The final predicate, strip_keys, simply removes the keys from the resulting list.

5.8 MEA

The other strategy offered with OPS5 is MEA. This is identical to LEX with one additional filter added. After refraction, it finds the time stamp associated with the first condition of the rule and picks the rule with the highest time stamp on the first condition. If there is more than one, then the normal LEX algorithm is used to pick which of them to use.

At first this might seem like an arbitrary decision; however, it was designed to make goal directed programming easier in OPS5. The flow of control of a forward chaining system is often controlled by setting goal facts in working storage. Rules might have goals in the conditions thus ensuring the rule will only fire when that goal is being pursued.

By making the goal condition the first condition on the LHS of each rule, and by using MEA, the programmer can force the system to pursue goals in a specified manor. In fact, using this technique it is possible to build backward chaining systems using a forward chaining tool.

The test for MEA is simply added to the system. First, the filter is added to the select_rule predicate. It will simply return the same conflict set if the current strategy is not MEA.

The actual filter predicates build the new list in an accumulator variable, Temp. If the first time stamp for a given rule is less than the current maximum, it is not included. If it equals the current maximum, it is added to the list of rules. If it is greater than the maximum, that timestamp becomes the new maximum, and the list is reinitialized to have just that single rule.

These examples illustrate some of the difficulties with expert systems in general. The OPS5 programmer must be intimately familiar with the nature of the inferencing in order to get the performance desired from the system. He is only free to use the tools available to him.

On the other hand, if the programmer has access to the selection strategy code, and knows the type of inferencing that will be required, the appropriate strategy can be built into the system. Given the accessibility of the above code, it is easy to experiment with different selection strategies.

Exercises

5.1 - Add full rule tracing to OOPS.

5.2 - Add a command loop which turns on and off tracing, MEA/LEX strategies, loads rule files, consults the rules, lists working storage, etc.

5.3 - Add a feature that allows for the saving of test case data which can then be run against the system. The test data and the results are used to debug the system as it undergoes change.

5.4 - Allow each rule to optionally have a priority associated with it. Use the user defined rule priorities as the first criteria for selecting rule instantiations from the conflict set.

5.5 - Add features on the LHS and RHS that allow rules to be written which can access the conflict set and dynamically change the rule priorities. Figure out an application for this.

5.6 - Add new syntax to the knowledge base that allows rules to be clustered into rule sets. Maintain separate conflict sets for each rule set and have the inference engine process each rule set to completion. Have higher level rules which can be used to decide which rule sets to execute. Alternatively, each rule set can have an enabling pattern associated with it that allows it to fire just as individual rules are fired.

5.7 - Each fact in working storage can be thought of as being dependent on other facts. The other facts are those which instantiated the LHS of a rule which udpated the fact. By keeping track of these dependencies, a form of truth maintenance can be added to the system. When a fact is then removed from working storage, the system can find other facts which were dependent on it and remove them as well.

Copyright ©1989,2000 Amzi! inc. All Rights Reserved.